Nicht so eindimensional! Vom Arbeiten mit multi-dimensionalen Daten

flatland (Quelle: https://xkcd.com/721/, Creative Commons Attribution-NonCommercial 2.5)

Dimensionen von Umweltdaten

Eindimensional

Bislang haben wir in diesem Kurs viel mit Zeitreihen gearbeitet. Zeitreihen sind ein Beispiel für eindimensionale Daten: Es wird die Dynamik einer oder mehrerer Variablen entlang der Dimension "Zeit" betrachtet.

Zweidimensional

In den Umweltwissenschaften haben wir es auch oft mit mehrdimensionsionalen Daten zu tun: So sind Umweltvariablen wie z.B. die Geländehöhe typischerweise entlang von zwei horizontalen Raumdimensionen ausgeprägt. Einen entsprechenden Datensatz nennt man dann typischerweise ein "Digitales Geländemodell" (DGM).

Dreidimensional

Während man die Geländehöhe über bestimmte Zeiträume als konstant annehmen kann, sind viele Umweltvariablen variabel in der Zeit und im horizontalen Raum. Beispiele sind Niederschlag, Landbedeckung, Bodenfeuchte u.v.a. Solche Daten lassen sich dann dreidimensional strukturieren, wobei die erste Dimension oft die Zeitdimension ist und die beiden anderen Dimensionen den horizontalen Raum abbilden. Das folgende Bild zeigt z.B. den zeitlichen Verlauf der Waldbedeckung in Borneo.

Ein anderes Beispiel für einen dreidimensionalen Datensatz ist der Zustand eines Systems entlang aller drei Raumdimensionen, also z.B. die Temperatur der Atmosphäre in Länge, Breite und Höhe, oder die Bodenfeuchte in einem Einzugsgebiet in unterschiedlichen Tiefen.

n-dimensional

Es kann sinnvoll sein, noch weitere Dimensionen hinzuzufügen. Wenn man in einem Klimamodell der Zustand der Atmosphäre in den drei Raumdimensionen sowie der Zeit darstellt und dann noch unterschiedliche Realisationen eines Modellensembles in einem Datensatz darstellt, so hätte man z.B. fünf Dimensionen.

Aufgabe

Ein "array" ist, einfach gesagt, ein Datensatz mit einheitlichem Datentyp entlang beliebig vieler Dimensionen. Gib aus den folgenden mehrdimensionalen Arrays folgende Werte an:

  • 1D-Array: zweites Element
  • 2D-Array: zweite Zeile, dritte Spalte
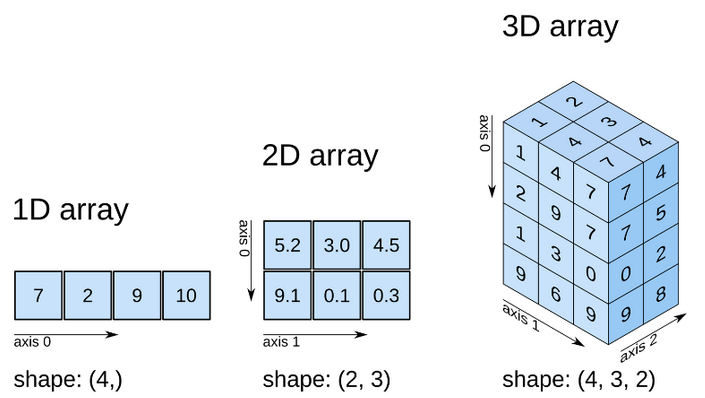
  • 3D-Array: zweite Zeile, zweite Spalte, äh...erste Spalte von der anderen Sorte Spalte?! multi

Ihr seht: Allein die Terminologie wird ab der dritten Dimension nicht ganz trivial. Der Einfachheit halber bietet es sich an, die Dimensionen einfach durchzunummerieren. In Python ist jedoch stets zu beachten: Beim durchnummerieren wird bei 0 begonnen...gucken wir uns gleich in Ruhe an.

numpy - multi-dimensionale Daten effizient verarbeiten

numpy ist in Python das Schlüsselmodul zum Arbeiten mit arrays entlang beliebiger Dimensionen. Kern ist der numpy.ndarray (nd steht für "n-dimensional") als Datentyp, der in unzähligen anderen Paketen zugrundegelegt wird.

In [1]:
import numpy as np
In [2]:
type( np.array([1,2,3]) )
Out[2]:
numpy.ndarray

Zum Aufwärmen: numpy in einer Dimension

In [3]:
# 1-D Array aus einer Liste erstellen
a = np.array([1,2,3,4])

Nehmen wir diesen Array einmal unter die Lupe:

In [4]:
print(a)
print("Number of dimensions:", a.ndim)

[1 2 3 4]
Number of dimensions: 1

Elemente eines Arrays ansprechen: im Prinzip genauso wie bei einer list

In [5]:
# Das zweite Element ansprechen ( Index 1 entspricht der zweiten Position!!)
a[1]
Out[5]:
2
In [6]:
# Das letzte Element ansprechen
a[-1]
Out[6]:
4
In [7]:
# Alle Elemente ansprechen
a[:]
Out[7]:
array([1, 2, 3, 4])
In [8]:
# Von der zweiten bis zur dritten Position
# ACHTUNG: Man gibt als rechte Grenze also immer die Position an, die NICHT in der Auswahl enthalten sein soll
a[1:3]
Out[8]:
array([2, 3])
In [9]:
# Von Anfang bis zur dritten Position
a[:3]
Out[9]:
array([1, 2, 3])
In [10]:
# Ab der zweiten Position
a[1:]
Out[10]:
array([2, 3, 4])
In [11]:
# Von der zweiten bis zur vorletzten Position
a[1:-1]
Out[11]:
array([2, 3])

Elemente eines Arrays manipulieren

In [12]:
# Werte von Elementen ändern
a[1] = 99
a
Out[12]:
array([ 1, 99,  3,  4])
In [13]:
# Mehrere Elemente auf einmal ändern
a[:2] = 999
a
Out[13]:
array([999, 999,   3,   4])

Mit Arrays arbeiten

Der große Unterschied zum Datentyp list: Man kann mit Arrays rechnen.

In [14]:
# Addition von zwei Listen
[1,2,3] + [1,2,3]
Out[14]:
[1, 2, 3, 1, 2, 3]
In [15]:
# Addition von zwei Arrays
np.array([1,2,3]) + np.array([1,2,3])
Out[15]:
array([2, 4, 6])
In [16]:
# Einen array mit aufsteigenden Werte erstellen
b = np.arange(5)
# Einen array aus Einsen erstellen, genauso lang wie `b`
c = np.ones(len(b))
print("b = ", b)
print("c = ", c)
# Eine Operation mit diesen Arrays
print("b + 2 * c = ", b + 2 * c)

b =  [0 1 2 3 4]
c =  [1. 1. 1. 1. 1.]
b + 2 * c =  [2. 3. 4. 5. 6.]

Aufgabe

Wir definieren folgenden Array:

test = np.array([0, 1, 10, 22, 3, 99])

Sage nun den Output folgender Operationen voraus (schreibe die Lösung auf ein Papier):

  • test[1]
  • test[-1]
  • test[0:3] * 2
  • test - test
  • test[2:-1]
  • test - np.arange(len(test)

Überprüfe nun Deine Lösung, indem Du in der untenstehenden Zelle den Array definierst und dann die Operationen ausführst. Vieviel Prozent hast Du richtig vorhergesagt?

Lösung

In [17]:
test = np.array([0, 1, 10, 22, 3, 99])
print(test[1])
print(test[-1])
print(test[0:3] * 2)
print(test - test)
print(test[2:-1])
print(test - np.arange(len(test)))

1
99
[ 0  2 20]
[0 0 0 0 0 0]
[10 22  3]
[ 0  0  8 19 -1 94]

Exkurs: Funktionen vs. Methoden

Du hast jetzt schon des Öfteren mit "Funktionen" und "Methoden" gearbeitet. Du kannst Dir eine Methode vorstellen wie eine Funktion, die an einem Objekt, z.B. an einem ndarray, einem DataFrame oder einem str "dranhängt". Oft ist es egal, ob Du ein Objekt mit seiner Methode oder der entsprechenden Funktion verarbeitet.

Unverständlich? Also lieber am Beispiel:

In [18]:
# Ein Array
x = np.array([1,2,3])
In [19]:
# Anwendung der Funktion "sum"
np.sum(x)
Out[19]:
6
In [20]:
# Anwendung der Methode "sum"
x.sum()
Out[20]:
6
In [21]:
# Am Beispiel eines Strings
x = "Neiekoelaeuese"
# Methode replace
print( x.replace("e","") )
# Funktion replace
print( str.replace(x, "e", "") )

Nikolaus
Nikolaus

Fazit: Meist ist es egal, ob Du eine Funktion oder eine Methode anwendest. Oft ist es bequemer, die Methode zu verwenden, aber nicht alle Funktionen stehen als Methoden zur Verfügung. Wie immer gilt: Alles Gewöhnungssache.

numpy-Arrays mit mehreren Dimensionen

Wir bringen uns in shape

In [22]:
# Wir erstellen zunächst 1-D array 
d1 = np.arange(24)
d1
Out[22]:
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23])
In [23]:
# Und machen aus diesem einen 3-D array
#   - mit 2 Elementen in der ersten Dimension,
#   - 3 in der zweiten,
#   - 4 in der dritten
d3 = d1.reshape((2,3,4))
d3
Out[23]:
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
In [24]:
d1.ndim, d3.ndim
Out[24]:
(1, 3)

Mit dem reshape-Befehl kann man also einen Array in "Form" bringen, ihm also eine andere Dimension geben.

Wir können die "Form" des Arrays mit dem shape Befehl überprüfen.

In [25]:
d3.shape
Out[25]:
(2, 3, 4)

Elemente auswählen

Das Ansprechen der Elemente eines mehrdimensionalen Arrays folgt im Prinzip der Intuition, kann aber schnell zum Braintwister werden...schaut's Euch am Besten in Ruhe an.

In [26]:
d3[:]
Out[26]:
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
In [27]:
d3[0,:,:]
Out[27]:
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
In [28]:
d3[0,1:3,:]
Out[28]:
array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
In [29]:
d3[0,1:3,2:4]
Out[29]:
array([[ 6,  7],
       [10, 11]])

Ansonsten funktioniert auch die Zuweisung genau so wie zuvor:

In [30]:
d3[0,1:3,2:4] = -99
d3
Out[30]:
array([[[  0,   1,   2,   3],
        [  4,   5, -99, -99],
        [  8,   9, -99, -99]],

       [[ 12,  13,  14,  15],
        [ 16,  17,  18,  19],
        [ 20,  21,  22,  23]]])
In [31]:
# Wir können auch mit Boolschen Arrays mit gleichem shape auswählen
d3[d3>18]
Out[31]:
array([19, 20, 21, 22, 23])

Aufgabe

Stelle Dir den folgenden 3-D Array x mal als eine Zeitreihe von Niederschlagsgittern vor, also einer flächenhaften Darstellung des Niederschlags über die Zeit. Sagen wir: 4 Zeitschritte, 3 Zeilen, 2 Spalten.

In [32]:
np.random.seed(42)
x = np.random.lognormal(1, 2, size=(4,3,2)).astype(int)
x
Out[32]:
array([[[ 7,  2],
        [ 9, 57],
        [ 1,  1]],

       [[63, 12],
        [ 1,  8],
        [ 1,  1]],

       [[ 4,  0],
        [ 0,  0],
        [ 0,  5]],

       [[ 0,  0],
        [50,  1],
        [ 3,  0]]])

Wähle nun der Reihe nach folgende Elemente aus:

  • Alle Elemente des dritten Zeitschritts
  • Alle Elemente der zweiten Spalte
  • Im zweiten Zeitschritt die zweite Zeile und erste Spalte
  • Alle Elemente > 0

Lösung

In [33]:
print(x[2])
print(x[:,:,1])
print(x[1,1,0])
print(x[x>0])

[[4 0]
 [0 0]
 [0 5]]
[[ 2 57  1]
 [12  8  1]
 [ 0  0  5]
 [ 0  1  0]]
1
[ 7  2  9 57  1  1 63 12  1  8  1  1  4  5 50  1  3]

Die axis des Guten - Funktionen entlang von Dimensionen anwenden

Eine große Stärke von numpy ist die Anwendung von Funktionen entlang einer Dimension. Auch hier lieber am Beispiel der Funktion sum:

In [34]:
x = np.ones((3,2), dtype="int")
x
Out[34]:
array([[1, 1],
       [1, 1],
       [1, 1]])
In [35]:
# Summe ALLER Elemente
x.sum()
Out[35]:
6
In [36]:
# Summe über alle Zeilen (axis = 0)
x.sum(axis=0)
Out[36]:
array([3, 3])
In [37]:
# Summe über alle Spalten (axis = 1)
x.sum(axis=1)
Out[37]:
array([2, 2, 2])

Das axis-Argument spezifiziert also immer die Dimension (Achse), die durch eine Operation "wegfallen" soll. Diese Funktionalität ist sehr mächtig und vor allem schnell und bequem.

Aufgabe

Nehmen wir einmal an, beim Array x handelt es sich um Messdaten für 10 Zeitschritte für 5 Sensoren. Wir stellen uns mal einen Beispieldatensatz her:

In [38]:
x = np.random.uniform(-1, 1, size=(10,5)).round(1)
x[x < 0] = np.nan
x
Out[38]:
array([[ 0.2,  nan,  0.2,  nan,  nan],
       [ 0.9,  0.9,  0.6,  nan,  nan],
       [ 0.4,  nan,  nan, -0. ,  nan],
       [ 0.8,  nan,  0.3,  nan,  0. ],
       [ 0.1,  nan,  0.9,  0.6,  0.9],
       [ 0.8,  0.2,  0.8,  nan,  nan],
       [ nan,  nan,  nan,  nan,  0.7],
       [ nan,  nan,  0.1,  nan,  0.6],
       [ nan,  1. ,  0.5,  nan,  nan],
       [ 0.6,  0.4,  0.5,  0.5,  nan]])

Leider fallen die Sensoren oft aus. Du möchtest Dir einen Überblick über die Datenverfügbarkeit verschaffen. Gebe für jeden Zeitschritt die Summe der Fehlwerte aus. Nutze dafür zunächst np.isnan und dann np.sum

Lösung

In [39]:
np.isnan(x).sum(axis=1)
Out[39]:
array([3, 2, 3, 2, 1, 2, 4, 3, 3, 1])

Wie bekomme ich überhaupt meine Daten in einen numpy-Array?

Es gibt viele Möglichkeiten, Daten in einen ndarray zu bringen. Im Wesentlichen unterscheiden wir zwei Szenarien:

  1. Array selbst erstellen
  2. Daten aus Dateien einlesen

Arrays selbst erstellen

Wir haben bereits verschiedene Wege kennengelernt, Arrays mit einem definierte shape zu erstellen und damit weiterzuarbeiten.

In [40]:
# Array aus Einsen
np.ones(shape=(2,2), dtype=int)
Out[40]:
array([[1, 1],
       [1, 1]])
In [41]:
# Array aus Nullen
np.zeros(shape=(2,2), dtype=int)
Out[41]:
array([[0, 0],
       [0, 0]])
In [42]:
# Länge des Arrays sowie Start- und Endpunkt (beide inklusive) vorgeben
np.linspace(start=1, stop=11, num=5)
Out[42]:
array([ 1. ,  3.5,  6. ,  8.5, 11. ])
In [43]:
# Start- und Endpunkt (exklusive) sowie Schrittweite vorgeben
np.arange(start=1, stop=11, step=2.5)
Out[43]:
array([1. , 3.5, 6. , 8.5])
In [44]:
# Zufallszahlen: Gleichverteilung
np.random.uniform(0,1,size=(2,2))
Out[44]:
array([[0.35846573, 0.11586906],
       [0.86310343, 0.62329813]])

Arrays aus Dateien einlesen

Bevor wir jetzt viele Beispiele behandelt: Die meisten Pythonpakete, die regelmäßige, mehrdimensionale Daten aus Dateien einlesen, geben diese als ndarray zurück. Das können Pakete zum Einlesen von Rasterdaten, Bildern usw. sein. Wir lernen nun ein besonderes Format kennen, das im wissenschaftlichen Bereich große Bedeutung gewonnen hat: das NetCDF-Format ("Network Common Data Form").

Anwendungsbeispiel: Schneeklimatologie in Europa mit ERA5

ERA5 ist das jüngste globale Reanalyseprodukt des ECMWF (European Centre for Medium-Range Weather Forecasts). Aber was ist eigentlich eine Reanalyse? Schaut Euch bitte zunächst das folgende Video an, dass wir mit etwas jupyter-Hokuspokus direkt einbinden können.

In [45]:
from IPython.display import HTML
In [46]:
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/FAGobvUGl24" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')

/home/maik/miniconda3/envs/umweltdv/lib/python3.7/site-packages/IPython/core/display.py:724: UserWarning: Consider using IPython.display.IFrame instead
  warnings.warn("Consider using IPython.display.IFrame instead")
Out[46]:

Wir verwenden in diesem Kurs "ERA5-Land", ein räumlich höher aufgelöstes Spezialprodukt, welches Klimavariablen für die Landoberfläche bereitstellt. Die Daten sind zwar stündlich, aber wir nutzen das Produkt mit monatlichen Mittelwerten, um die Datenmenge zu reduzieren. Auch nutzen wir nur ein Fenster über Europa.

Die Daten können hier heruntergeladen werden - Ihr müsst Euch für den Download allerdings bei Copernicus registrieren. Aber das Formular für die Auswahl der Daten könnt Ihr Euch auch so anschauen. Eine Beschreibung der verfügbaren Parameter aus ERA5-Land gibt es hier.

Wir haben für unser Beispiel die Parameter Schneebedeckung (snowc) und Temperatur in 2m Höhe (t2m) heruntergeladen. Das sind für Europa allein immerhin schon über 300 MB.

Lesen der Daten aus einer NetCDF-Datei

Ohne hier in die Tiefe zu gehen, lernen wir ein wichtiges Datenformat zur Speicherung mehrdimensionaler Daten kennen, das netcdf-Format. Wir nutzen dazu das Paket netCDF4.

In [47]:
import netCDF4 as nc
In [48]:
era5 = nc.Dataset("../data/era5_2mtemp_and_snowcover.nc", "r", format="NETCDF4")

Das Besondere am NetCDF-Format ist, dass die Daten bereits entlang der Dimensions strukturiert sind. Diese Dimesionen kann man sich wie folgt anzeigen lassen:

In [49]:
era5.dimensions
Out[49]:
{'longitude': <class 'netCDF4._netCDF4.Dimension'>: name = 'longitude', size = 401,
 'latitude': <class 'netCDF4._netCDF4.Dimension'>: name = 'latitude', size = 401,
 'time': <class 'netCDF4._netCDF4.Dimension'>: name = 'time', size = 485}

Wir haben also die Dimensionen latitude, longitude und time. Entlang dieser Dimensionen kann eine NetCDF-Datei beliebig viele Variablen (i.e. Daten) bereithalten. Einen Überblick gibt uns das Attribut variables.

In [50]:
era5.variables
Out[50]:
{'longitude': <class 'netCDF4._netCDF4.Variable'>
 float32 longitude(longitude)
     units: degrees_east
     long_name: longitude
 unlimited dimensions: 
 current shape = (401,)
 filling on, default _FillValue of 9.969209968386869e+36 used,
 'latitude': <class 'netCDF4._netCDF4.Variable'>
 float32 latitude(latitude)
     units: degrees_north
     long_name: latitude
 unlimited dimensions: 
 current shape = (401,)
 filling on, default _FillValue of 9.969209968386869e+36 used,
 'time': <class 'netCDF4._netCDF4.Variable'>
 int32 time(time)
     units: hours since 1900-01-01 00:00:00.0
     long_name: time
     calendar: gregorian
 unlimited dimensions: 
 current shape = (485,)
 filling on, default _FillValue of -2147483647 used,
 't2m': <class 'netCDF4._netCDF4.Variable'>
 int16 t2m(time, latitude, longitude)
     scale_factor: 0.0009662785982020747
     add_offset: 280.1167577664626
     _FillValue: -32767
     missing_value: -32767
     units: K
     long_name: 2 metre temperature
 unlimited dimensions: 
 current shape = (485, 401, 401)
 filling on,
 'snowc': <class 'netCDF4._netCDF4.Variable'>
 int16 snowc(time, latitude, longitude)
     scale_factor: 0.0015259487586406848
     add_offset: 49.99923702562068
     _FillValue: -32767
     missing_value: -32767
     units: %
     long_name: Snow cover
 unlimited dimensions: 
 current shape = (485, 401, 401)
 filling on}

Aufgabe

Du siehst, dass auch die Dimensionen als Variablen abgelegt sind. Schau Dir nun den Output des Befehls era5.variables genauer an: Welche Einheiten haben die Variablen - und welchen shape?

Lösung

  • longitude, unit: degrees east, shape: (401,)
  • latitude, unit: degrees north, shape: (401,)
  • time, unit: hours since 1900-01-01 00:00:00.0, shape: (485,)
  • t2m (2 metre temperature), units: Kelvin, shape: (485, 401, 401)
  • snowc (Snow cover), unit: %, shape: (485, 401, 401)

Analyse der Schneebedeckung

In [51]:
import matplotlib.pyplot as plt

Um einen groben Überblick über die räumlichen Verhältnisse zu erhalten, berechnen wir zunächst den Mittelwert der Schneebedeckung (snowc) über den gesamten Zeitraum für jede Gitterzelle. Da die Zeit die erste Dimension ist, berechnen wir den Mittelwert (mean) entlang der ersten Dimension (axis=0).

Wir sehen an diesem Beispiel auch gleich, wie wir auf die Daten im NetCDF zugreifen: {NetCDF-Objekt}["{Variable}"][:].

Das nachgestellte [:] ist der Schlüssel, um auf die Daten als ndarray zuzugreifen. Von da an ist alles Routine...

In [52]:
snowc_time_avg = era5["snowc"][:].mean(axis=0)

Eine schnelle Möglichkeit zum Plotten regelmäßiger Gitter bietet die matplotlib-Funktion imshow.

In [53]:
cp = plt.imshow(snowc_time_avg)

Wir würden hier gern noch die Achsen mit sinnvollen Ticklabels versehen. Dafür gibt es unterschiedliche Kniffe. Wir geben hier einfach die räumliche Bounding Box ([x_min , x_max, y_min , y_max]) an, die wir aus den Variablen latitude und longitude konstruieren.

In [54]:
bbox = [era5["longitude"][:].min(),
        era5["longitude"][:].max(),
        era5["latitude"][:].min(),
        era5["latitude"][:].max()]

Also nochmal in schicker...

In [55]:
fig = plt.figure(figsize=(8,8))
cmap = plt.cm.get_cmap("Greens_r").copy()
cmap.set_bad('black',1.)
cp = plt.imshow(snowc_time_avg, extent=bbox, cmap=cmap)
#fig.set_facecolor("black")
plt.xlabel("Latitude")
plt.xlabel("Longitude")
plt.grid()
plt.colorbar(cp, shrink=0.8)
_ = plt.title("Average snow cover (%) from 1981-2021")

Aufgabe

Stelle nun den Zusammenhang zwischen Breitengrad und Schneebedeckung dar, mit anderen Worten: Berechne den Mittelwert der Schneebedeckung entlang der Dimensionen time und longitude und plotte dann den resultieren 1-D Array gegen die Dimension latitude. Hinweis: Das axis-Argument kann mehrere Dimensionen enthalten. Mit axis=(0,1) "reduziert" man z.B. die Dimensionen 0 und 1 gleichzeitig.

Lösung

In [56]:
snowc_time_long_avg = era5["snowc"][:].mean(axis=(0,2))
In [57]:
plt.plot(era5["latitude"][:], snowc_time_long_avg)
plt.xlabel("Latitude")
plt.ylabel("Avg. snow cover (%)")
plt.grid()

Vertiefungsaufgabe

Mal wieder Klimawandel: Stelle den zeitlichen Verlauf der mittleren Schneebedeckung dar. Dafür brauchst Du einen datetime Array. Die Variable time ist ein bisschen spröde...sie stellt Stunden seit dem 1. Januar 1900 dar. Die Umwandlung in einen Array von datetime schenken wir Dir...und nehmen pandas zur Hilfe.

In [58]:
import pandas as pd
In [59]:
dtimes = pd.to_datetime(era5["time"][:].astype(np.int64)*3600, unit="s", origin="1900-01-01T00:00:00")

Anmerkung: Wer sich fragt, warum wir nochmal eine Typkonvertierung mit astype(np.int64) machen, kann diese ja mal rauslöschen und schauen, was passiert. Stichwort: Overflow. Die Aufklärung für Streber:innen gibt es passenderweise bei Stackoverflow. Gut, dass wir wissen, was Datentypen sind...

So, jetzt bist Du dran!

Lösung

In [60]:
snowc_lat_long_avg = era5["snowc"][:].mean(axis=(1,2))
In [61]:
plt.rcParams.update({'font.size': 14})
plt.subplots(figsize=(12,5))
plt.plot(dtimes, snowc_lat_long_avg)
plt.xlabel("Time")
plt.ylabel("Avg. snow cover (%)")
plt.grid()

Wir sehen hier einen klaren Jahresgang, vielleicht auch einen gewissen Trend über die Zeit? Naja, ganz schön schwierig mit den Trends, vor allem wenn die Reihe "nur" 40 Jahre lang ist. Außerdem ist zu bedenken: Es geht um Schneebedeckung, nicht um Schmelzwasseräquivalente...naja. Vertagen wir das Thema.

Wer noch Lust hat, kann ja mal ein paar statistische Kennwerte über die Zeit für eine Teilregion betrachten - sagen wir mal eine grobe Definition für Mitteleuropa: alles zwischen 5 und 15 Grad West und 45 und 55 Grad Nord.

In [62]:
i = np.where(era5["latitude"][:]==55.)[0][0]
j = np.where(era5["latitude"][:]==45.)[0][0]
k = np.where(era5["longitude"][:]==5.)[0][0]
m = np.where(era5["longitude"][:]==15.)[0][0]
i, j, k, m
Out[62]:
(150, 250, 150, 250)
In [63]:
snowc_me = era5["snowc"][:,i:j, k:m].mean(axis=(1,2))

Für die Statistik packen wir das lieber in einen DataFrame.

In [64]:
df = pd.DataFrame({"snowc":snowc_me}, index=dtimes)

Jetzt wollen wir für jedes Jahr den Mittelwert und das Maximum der Schneebedeckung darstellen.

In [65]:
# Das letzte Jahr schmeißen wir raus, weil unvollständig
dfmean = df.resample("1a").mean()[:-1]
dfmax = df.resample("1a").max()[:-1]
In [66]:
plt.rcParams.update({'font.size': 14})
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(dfmean.index, dfmean.snowc, color="tab:blue", lw=1.5, label="Mean SC per year")
plt.plot(dfmax.index, dfmax.snowc, color="tab:red", lw=1.5, label="Max. SC per year")
plt.xlabel("Time")
plt.ylabel("Snow cover (%)")
plt.legend()
plt.grid()

Naja, sieht ein bisschen langweilig aus...aber so ist das eben manchmal.

In [ ]: