Arbeiten mit DataFrames: local global warming...¶

Die Säkularstation in Potsdam¶
Wir arbeiten in dieser Lektion mit einer legendären Zeitreihe, die direkt vor unserer Haustür liegt: Den Aufzeichnungen der sog. Säkularstation auf dem Telegraphenberg in Potsdam. Hier werden seit über 100 Jahren Klimabeobachtungen aufgezeichnet. Wir wollen uns auf die Beobachtungen der bodennahen Temperatur und der relativen Luftfeuchte beschränken.
Bei so einer langen Zeitreihe stellt sich gleich die Frage, ob wir den Effekt der lokalen Erwärmung sehen können...aber eins nach dem anderen.
Die Daten werden über das opendata-Portal des DWD bereitgestellt. Die Säkularstation hat die ID 03987. Die Zeitreihe findet Ihr unter ../data/saekularstation/produkt_tu_stunde_18930101_20201231_03987.txt als csv-Datei.
Aufgabe: Daten einlesen¶
Zum Einlesen dieser Daten nutzen wir das Paket pandas, das Ihr bereits kurz in Lektion 1 kennengelernt habt.
import pandas as pd
Genauer gesagt nutzen wir die Funktion pd.read_csv. Ruft doch einmal die Hilfe zu dieser Funktion auf.
- Über welchen Parameter teilt Ihr der Funktion mit, welches Zeichen in der Datei als Spaltentrenner verwendet wird?
- Und welches Zeichen wird nun in der Datei als Spaltentrenner verwendet?
- Lest auf Grundlage dieser Erkenntnis die Datei als DataFrame mit Namen
dfein.
Lösung¶
df = pd.read_csv("../data/saekularstation/produkt_tu_stunde_18930101_20201231_03987.txt", sep=";")
Aufgabe: Erkunden des Dataframes¶
Nutze die Funktionen, die du im ersten Teil kennengelernt hast, zum Erkunden des Dataframes.
- Wieviele Zeilen und Spalten hat der Dataframe?
- Welche Struktur hat der Dataframe? Was gibt es für Spalten, was bedeuten sie?
- Lass Dir die ersten und letzten Zeilen des Dataframes sowie eine Zusammenfassung der Spalten anzeigen.
Lösung¶
# Zeilen, Spalten
df.shape
df.info()
df.head()
df.tail()
df.describe()
Datum und Zeit im DateFrame¶
Wir wollen unseren DataFrame zunächst ein wenig aufräumen: weniger sperrige Spaltennamen verwenden und Spalten rausschmeißen, die in unserem Kontext nicht brauchen.
# Etwas weniger sperrige Spaltennamen verwenden
df.columns = ['id', 'datetime', 'qn9', 'temp', 'rh', 'eor']
# Nur die Spalten mit Datum, Temperatur und relativer Luftfeuchte behalten
df = df[["datetime", "temp", "rh"]]
Ein schneller Plot...
df.temp.plot()
Ein ganz schönes Gezappel, aber gut: Es sind ja auch über 100 Jahre stündlicher Daten! Was wir aber vermissen: die Zeitinformation auf der x-Achse. Dazu fehlen zwei Schritte:
Zunächst müsen wir
pandasmitteilen, dass es die Spaltedatetimeauch als Datum interpretieren soll. Bisher sind das einfach Strings, also Zeichenketten. Dazu nutzen wir die Funktionpd.to_datetime.Nun wollen wir, dass die Spalte
datetimenicht nur irgendeine Spalte sei, sondern das primäre "Label" einer Zeile ...nämlich derindex. Dazu nutzen wirset_index.
# datetime-Spalte auch als datetime interpretieren
df.datetime = pd.to_datetime(df.datetime, format="%Y%m%d%H")
# datetime als index verwenden
df = df.set_index("datetime")
df.temp.plot()
Ja, so ist's besser. Wir schauen uns nochmal den "Kopf" des DataFrames an und sehen, dass die Spalte datetime jetzt als Index fungiert.
df.head()
Die Spalte datetime lässt sich nun auch nicht mehr über den Spaltennamen aufrufen...Ihr erhaltet einen AttributeError - aua.
df.datetime
...sondern über das index-Attribut:
df.index
Aufgabe¶
Nur zur Erinnerung an frühere Zeiten: versucht doch mal, den Datensatz in Excel oder OpenOffice Calc einzulesen und die obige Abbildung zu reproduzieren.
Lösung¶
Ich hab es mal in OpenOffice Calc probiert...mit folgendem Ergebnis:
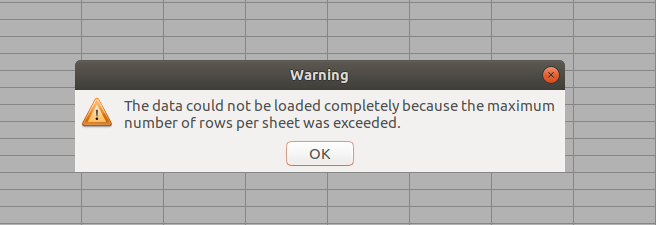
Jahresmittelwerte darstellen¶
Wie oben schon angesprochen, sieht man bei über 100 Jahren stündlicher Daten erstmal nicht so viel. Schauen wir uns doch mal die Zeitreihe der Jahresmittelwerte an. Die geht in pandas sehr komfortabel mit Hilfe der resample-Funktion.
resample¶
Kern der resample-Funktion ist das Zeitinterval, auf welchem die Mittelung stattfinden soll. Anschließend teilt man pandas mit, welche Funktion denn auf diesem Zeitintervall angewendet werden soll. Hier wäre das die Funktion mean. Das Ergebnis ist ein neuer DataFrame, den wir hier dfa nennen.
# Jahresmittelwerte ("1a")
dfa = df.resample("1a").mean()
dfa.info()
dfa.temp.plot()
Abbildungen zurechtbasteln¶
Die obige Abbildung sieht ja schon ganz gut aus - v.a. beeindruckend, was das Erwärmungssignal angeht. Wir wollen aber ein paar Möglichkeiten kennenlernen, Abbildungenseigenschaften zu kontrollieren. Eine kleine Auswahl der Plot-Elemente gibt die folgende Abbildung:
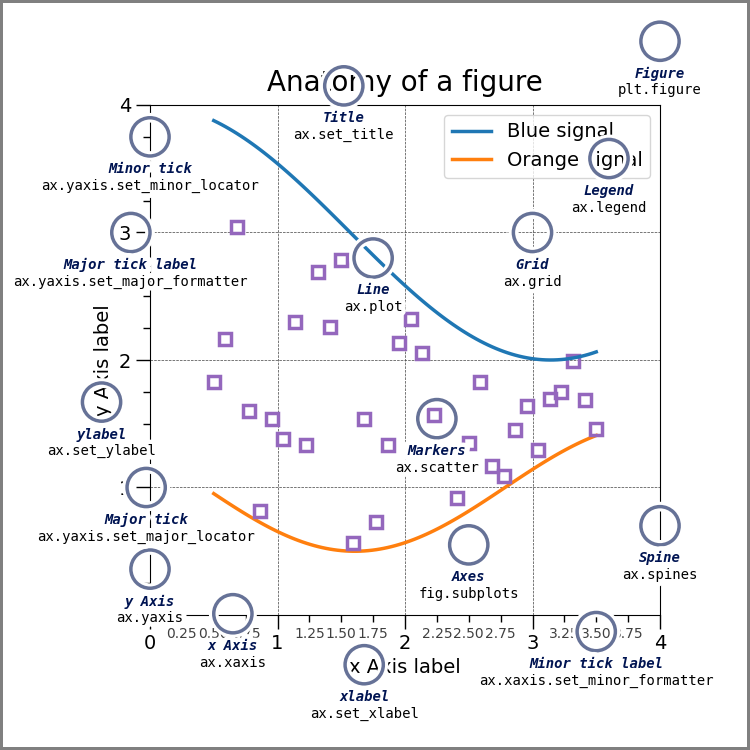
Grundsätzlich ist das Arbeitspferd für Abbildungen in Python matplotlib. Auch die plot-Funktion, die an den DataFrames dranhängt, baut auf matplotlib auf. Wir können matplotlib mit pandas auf beliebige Weise kombinieren. Dazu importieren wir zunächst das pyplot-Modul aus matplotlib.
import matplotlib.pyplot as plt
Wir versuchen gar nicht erst, uns die unterschiedlichen Plot-Eigenschaften und Manipulationsmöglichkeiten systematisch zu erarbeiten. Also lieber ein Beispiel mit Erläuterungen im Code.
# Wir machen von Anfang an klar, dass wir größere Beschriftungen haben wollen
# Kleine Labels sind ein stetes Ärgernis in Abbildungen
plt.rcParams.update({'font.size': 16})
# Wir erzeugen einen Canvas, also eine Leinwand, auf die wir pinseln:
# nrows: Zahl der Zeilen für subplots
# ncols: Zahl der Spalten für subplots
# figsize: Größe der gesamten Abbildung (Breite, Höhe)
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(10,5))
# Wir benutzen nun die originäre plot-Funktion aus matplotlib
plt.plot(dfa.index, dfa.temp, "-", color="tab:blue")
# fügen ein Gitter hinzu
plt.grid()
# ein Label für die y-Achse (x-Achse ist selbsterklärend)
plt.ylabel("Temperatur (°C)")
# einen Titel
plt.title("Jahresmitteltemperatur, Säkularstation Potsdam")
# ein Label
plt.plot(pd.to_datetime("1941-01-01"), dfa.temp.min(), "o", color="purple", ms=15, mfc="None")
plt.text(pd.to_datetime("1943-12-01"), 6.5, "Kältestes Jahr (1941)", color="purple")
# Noch ein Label
plt.plot(pd.to_datetime("2019-12-31"), dfa.temp.max(), "o", color="tab:red", ms=15, mfc="None")
plt.text(pd.to_datetime("2018-01-01"), 11.2, "Wärmstes Jahr (2019)",
horizontalalignment="right", color="tab:red")
# Grenzen ziehen
plt.xlim(pd.to_datetime("1893-01-01"), pd.to_datetime("2021-01-01"))
# Eine vertikale Linie zeichnen
plt.axvline(pd.to_datetime("1990-10-03"), ls="--", color="grey")
plt.text(pd.to_datetime("1992-01-01"), 6.5, "Wieder-\nvereinigung", color="grey")
Zitat von Brad Salomon:
"[...] there’s no getting around the fact that matplotlib can be a technical, syntax-heavy library. Creating a production-ready chart sometimes requires a half hour of Googling and combining a hodgepodge of lines in order to fine-tune a plot. [...] However, understanding how matplotlib’s interfaces interact is an investment that can pay off down the road."
- Die Möglichkeiten, an matplotlib plots herumzubasteln, sind unendlich
- interessante Tutorials:
axesist nicht zu verwechseln mitaxis- ...
Die zehn wärmsten Jahre¶
Da wir nun schon einen DataFrame mit den Jahresmitteltemperaturen haben, können wir uns auch gleich die zehn wärmsten Jahre raussuchen. Wir nutzen dafür den Befehl sort_values. Der Parameter by bestimmt, nach welchem Merkmal sortiert wird, der Parameter ascending... - naja, is klar, oder? Das Ergebnis ist wiederum ein DataFrame, aus dem wir die ersten zehn Einträge auswählen.
# Die 10 wärmsten Jahre seit 1893
dfa.sort_values(by=["temp"], ascending=False)[0:10]
Tja, da hat sich tatsächlich ein Jahr reingeschlichen, das nicht im 21. Jahrhundert liegt. Jaja, das Jahr 1934 war aber auch wirklich ein warmes, ich weiß es noch genau.
Aufgabe: Winter is not coming¶
Wieviel Jahre aus dem 21. Jahrhundert gehören zu den zehn kältesten Jahren der Zeitreihe? Ihr dürft auch raten...nee, doch nicht.
Lösung¶
# Die 10 kältesten Jahre seit 1893
dfa.sort_values(by=["temp"], ascending=True)[0:10]
Antwort also: nicht ein einziges Jahr!
Mitteltemperatur für Klimanormalperioden¶
Der Bezugszeitraum für die Berechnung statistischer Kennwerte des Klimas ist die Klimanormalperiode. Die aktuelle Normalperiode ist 1991-2020. Man kommt bei Klimabeobachtungen nicht oft in den Genuss, vier Normalperioden miteinander vergleichen zu können. Bei der Säkularstation ist das möglich.
In pandas können wir mit Hilfe des datetime-index sehr komfortabel Zeiträume auswählen. pandas erkennt dabei normalerweise gut, was für Zeitelemente wir dabei meinen. Im folgenden Beispiel reicht die Angabe der Jahre:
# Mitteltemperatur in Potsdam für Normalperiode 1991-2020
df.loc["1991":"2020"].temp.mean()
Aufgabe: Vergleich der Normalperioden und "Special Feature" zu String-Formatierung¶
Berechne die Mitteltemperatur für die Klimanormalperioden 1901-1930, 1931-1060, 1961-1990 und 1991-2020.
- Welches war die wärmste Normalperiode?
- Welches die kälteste?
- Wie groß ist Differenz zwischen wärmster und kältester Normalperiode?
- Wie groß ist die Differenz zwischen der aktuellen und der vergangenen Normalperiode?
Kleines Extra für Eure Lösung: string formatting. Lernt, wie Ihr Zahlen und Zeichenketten effizient zu Strings zusammensetzen könnt. Wie haben ja schon gelernt, dass man strings mit dem +-Zeichen verketten kann. Aber es geht noch besser. Am Besten am Beispiel:
# Strings einbetten
name = "Säkularstation"
print("Name der Station: %s" % name)
# Floats einbetten, hier gerundet auf zwei Dezimalstellen
lat = 52.3813
lon = 3.0622
print("Standort der %s: %.2f geogr. Länge, %.2f geogr. Breite." % (name, lon, lat))
# Integer einbetten
print("Länge der Zeitreihe am Standort %s: %d Stunden" % (name, len(df)))
# Datumsformat einbetten
# (das werden wir später nochmal ausführlich machen)
print("Erste Stunde in der Zeitreihe am Standort %s: %s Uhr UTC" % (name, df.index[0].strftime("%d. %B %Y, %H:%M") ) )
Versucht nun also die Antworten auf die obigen Fragen mit Hilfe der String-Formatierung via print "auszudrucken".
Lösung¶
avgT1901 = df["1901":"1930"].temp.mean()
avgT1931 = df["1931":"1960"].temp.mean()
avgT1961 = df["1961":"1990"].temp.mean()
avgT1991 = df["1991":"2020"].temp.mean()
print("Mitteltemperaturen der Klimanormalperioden:")
print(" 1901-1930: %.1f °C(kälteste)" % avgT1901)
print(" 1931-1960: %.1f °C" % avgT1931)
print(" 1961-1990: %.1f °C" % avgT1961)
print(" 1991-2020: %.1f °C (wärmste)" % avgT1991)
print()
print("Differenzen zwischen den Mittelwerten:")
print(" Wärmste NP (1991-2020) - kälteste NP (1901-1930): %.1f °C" % (avgT1991-avgT1901))
print(" avgT(1991-2020} - avgT(1961-1990): %.1f °C" % (avgT1991-avgT1961))
print("")
print("What do we want: climate justice! When do we want it: now!")
Nochmal die Abbildung: nun mit den Mittelwerten der Normalperioden¶
plt.rcParams.update({'font.size': 16})
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(10,5))
plt.plot(dfa.index, dfa.temp, "-", color="tab:blue")
#plt.grid()
plt.ylabel("Temperatur (°C)")
#plt.title("Jahresmitteltemperatur, Säkularstation Potsdam")
plt.xlim(pd.to_datetime("1893-01-01"), pd.to_datetime("2021-01-01"))
# Grenzen der Normalperioden einzeichnen
plt.axvline(pd.to_datetime("1901-01-01"), ls="-", color="tab:red")
plt.axvline(pd.to_datetime("1931-01-01"), ls="-", color="tab:red")
plt.axvline(pd.to_datetime("1961-01-01"), ls="-", color="tab:red")
plt.axvline(pd.to_datetime("1991-01-01"), ls="-", color="tab:red")
plt.axvline(pd.to_datetime("2021-01-01"), ls="-", color="tab:red")
# T-Mittelwerte der Normalperioden
plt.plot([pd.to_datetime("1901-01-01"), pd.to_datetime("1930-12-31")], [avgT1901, avgT1901], color="tab:red")
plt.plot([pd.to_datetime("1931-01-01"), pd.to_datetime("1960-12-31")], [avgT1931, avgT1931], color="tab:red")
plt.plot([pd.to_datetime("1961-01-01"), pd.to_datetime("1990-12-31")], [avgT1961, avgT1961], color="tab:red")
plt.plot([pd.to_datetime("1991-01-01"), pd.to_datetime("2020-12-31")], [avgT1991, avgT1991], color="tab:red")
# Betonung der Differenz zwischen letzter und aktueller NP
plt.plot([pd.to_datetime("1991-01-01"), pd.to_datetime("1991-01-01")],
[avgT1961, avgT1991], color="tab:red", lw=5, solid_capstyle="butt")
_ = plt.text(pd.to_datetime("1992-12-01"), 9.1, r"$\Delta$"+"T=%.1f °C" % (avgT1991-avgT1961),
fontsize=20, color="tab:red", bbox=dict(facecolor='white', alpha=0.5, edgecolor='None'))
Mittlere Tagesgänge¶
Ein weiteres der vielen beeindruckenden Features von pandas ist die groupby-Funktion. Sie erlaubt es uns, die Einträge des DataFrames nach bestimmten Merkmalen zu gruppieren und für diese Gruppen dann Funktionen anzuwenden. Wir nutzen diese Funktionalität, um mit einer einzigen Zeile den mittleren Tagesgang von Temperatur und relativer Luftfeuchte in Potsdam zu ermitteln. Jetzt wissen wir auch, warum wir die ganze Zeit die Spalte rh mitgeschleppt haben.
# groupby zusammen mit der Stunde des Tages, die wir aus dem Zeitindex des DatFrame extrahieren
dfh = df.groupby(df.index.hour).mean()
dfh
Schöner sieht das natürlich in einer Abbildung aus. Wir wissen aber jetzt schon, dass wir Schwierigkeiten kriegen, wenn wir die Variable temp und relhum auf eine Achse plotten, da ihre Wertebereiche zu unterschiedlich sind (siehe Tabelle). Darum lernen wir bei dieser Gelegenheit die Sekundärachse kennen.
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(10,5))
tpl = plt.plot(dfh.index, dfh.temp, "-", color="tab:blue", label="T")
plt.ylabel("T (°C)")
# Hier kommt die Sekundärachse ins Spiel
plt.twinx()
rhpl = plt.plot(dfh.index, dfh.rh, "-", color="tab:red", label="RH")
plt.ylabel("Rel. Luftfeuchte (%)")
plt.title("Mittlerer Tagesgang in Potsdam: 1893-2021")
_ = plt.legend(handles=[tpl[0], rhpl[0]])
Aufgabe¶
Kleine Auffrischung aus der Angewandten Klimatologie im Bachelor: Erkläre Deinen Nachbar:innen, den Verlauf der beiden Kurven. Warum fällt das Temperaturmaximum nicht mit dem mittleren Sonnenhöchststand zusammen? Wie lässt sich der Verlauf der relativen Luftfeuchte erklären.
Lösung¶
Die Temperatur der Erdoberfläche steigt, wenn die Nettostrahlung positiv ist und sinkt, wenn sie negativ ist. Die Nettostrahlung wiederum ergibt sich aus der Differenz aus kurzwelliger Strahlungseinnahme (Globalstrahlung abzüglich Albedo) und effektiver langwelliger Ausstrahlung (Ausstrahlung abzüglich atmosphärischer Gegenstrahlung). Die Nettostrahlung ist positiv auch über den Sonnenhöchststand hinaus, wird im Laufe des Nachmittags negativ und erst eine Weile nach Sonnenaufgang wieder positiv. Desweiteren braucht es eine Weile, bis sich die Temperaturdynamik von der Oberfläche bis in 2 m Messhöhe fortsetzt.
Die Dynamik der relativen Luftfeuchte
$RH = \frac{e}{E(T)}$
ist maßgeblich von der Temperatur getrieben, da der Sättigungdampfdruck $E(T)$ gemäß Magnus-Formel exponentiell von der Lufttemperatur $T$ abhängt. Die Dynamik der tatsächlichen Luftfuechte (z.B. ausgedrückt als Dampfdruck $e$) geht darin fast unter.
Mögliche Vertiefungen in der Coding-Werkstatt¶
Ermittle die Differenz der Mitteltemperatur zwischen den Normalperioden 1961-1990 und 1991-2020 für die Bergwetterwarte Hohenpeißenberg. Wo ist die Differenz größer: in Potsdam oder am Hohenpeißenberg?
Die Daten findet Ihr auf dem opendata-Server des DWD (Link). Ihr müsst in dem opendata-Verzeichnis allerdings erstmal rausfinden, in welcher Datei die Daten der Station Hohenpeißenberg liegen...
Berechne als zusätzliche Spalte des DataFrame
dfden Dampfdruck (in hPa). Mache Dir dazu die Definition der relativen Luftfeuchte zunutze. Verwende in erster Näherung die Magnusformel über ebenen Wasserflächen:$e = 6.112 * exp(\frac{17.61 * T}{243.12 + T})$
Stelle nun den mittleren Tagesgang der Temperatur und des Dampfdrucks dar!
- Etwas schwerer...stelle den mittleren Tagesgang der Temperatur in den Monaten Dez-Feb im Vergleich zu den Monaten Jun-Aug dar. Was fällt auf?